The CUNY Probability Seminar is typically held on Tuesdays from 4:15 to 5:15 pm at the CUNY Graduate Center Math Department. The exact dates, times and locations are mentioned below. If you want to talk at the seminar, or want to be added to/removed from the seminar mailing list, then please contact the Seminar Coordinator
Shirshendu Chatterjee (shirshendu at ccny dotcuny dotedu)
Tuesday, February 7, 4:15 PM, Rm. 5417
Speaker: Christian Benes, Brooklyn College, CUNY
Title: Where Planar Simple Random Walk Loses its Rotational Symmetry
Abstract: We present an explicit local limit theorem for simple random walk in dimensions 1 and 2, valid for all points in the range of the walk. The two-dimensional result allows to obtain a precise description of where and how planar simple random walk loses its approximate rotational symmetry.
Tuesday, February 21, 4:15 PM, Rm. 5417
Speaker: Daniel Ahlberg, IMPA, Brazil
Title: Random coalescing geodesics in first-passage percolation
Abstract: A random metric on
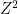
is obtained by assigning non-negative i.i.d. weights to the edges of the nearest neighbour lattice. We shall discuss properties of geodesics in this metric. We develop an ergodic theory for infinite geodesics via the study of what we shall call `random coalescing geodesics’. Random coalescing geodesics have a range of nice properties. By showing that they are (in some sense) dense is the space of geodesics, we may extrapolate these properties to all infinite geodesics. As an application of this theory we answer a question posed by Benjamini, Kalai and Schramm in 2003, that has come to be known as the `midpoint problem’. This is joint work with Chris Hoffman.
Tuesday, February 28, 4:15 PM, Rm. 5417
Speaker: Warren Tai, Graduate Center, CUNY
Title: Is the Riemann zeta function in a short interval a 1-RSB spin glass?
Abstract: Fyodorov, Hiary & Keating established an intriguing connection between the maxima of log-correlated processes and the ones of the Riemann zeta function on a short interval of the critical line. In particular, they suggest that the analogue of the free energy of the Riemann zeta function is identical to the one of the Random Energy Model in spin glasses. In this paper, the connection between spin glasses and the Riemann zeta function is explored further. We study a random model of the Riemann zeta function and show that its two-overlap distribution corresponds to the one of a one-step replica symmetry breaking (1-RSB) spin glass. This provides evidence that the local maxima of the zeta function are strongly clustered.
Tuesday, March 7, 4:15 PM, Rm. 5417
Speaker: Guillaume Barraquand, Columbia University
Title: ASEP on the positive integers with an open boundary.
Abstract: The asymptotic fluctuations of a large class of growth processes and one dimensional particle systems are predicted to follow probability distributions from random matrix theory with 1/3 scaling exponents. It is conjectured that the limit theorems are universal, in the sense that they do not depend on the microscopic details of the model. However, the geometry and boundary conditions have an influence on the nature of limiting statistics. In this talk, we will explore the situation in a half space. We will recall the general predictions for such systems and present new results about the asymmetric simple exclusion process when particles travel on the positive integers coming out of a reservoir at the origin. Joint work with Alexei Borodin, Ivan Corwin and Michael Wheeler.
Tuesday, March 14, 4:15 PM, Rm. 5417
The seminar is canceled because of an unavoidable circumstance.
Speaker: Victor de la Peña, Columbia University, Department of Statistics
Title: On Boundary Crossing By Stochastic Processes
Abstract: In this talk, we introduce an approach to bound the expected time for stochastic processes to cross a boundary. The approach can be thought as a direct extension of the concept of boundary crossing of non-random functions to that of stochastic processes. It can also be viewed as an extension of Wald’s equations in sequential analysis to the case of stochastic processes with arbitrary dependence structure.
Tuesday, March 21, 4:15 PM, Rm. 5417
Speaker: Kei Kobayashi, Fordham University
Title: Stochastic differential equations modeling anomalous diffusions
Abstract: Standard Brownian motion composed with the inverse of a stable subordinator has been used to model a subdiffusion, which is a type of an anomalous diffusion where particles spread more slowly than the classical Brownian particles. This new stochastic process is significantly different from the Brownian motion; for example, it is neither Markovian nor Gaussian and has transition probabilities satisfying a time-fractional order heat equation.
This talk focuses on stochastic differential equations (SDEs) driven by a L\’evy process composed with the inverse of a stable subordinator. We derive time-fractional Kolmogorov-type equations associated with the SDEs as well as justify the effectiveness of a numerical approximation scheme for the SDEs. This is joint work with Molly Hahn, Ernest Jum and Sabir Umarov.
Tuesday, March 28, 4:15 PM, Rm. 5417
Speaker: Konstantin Tikhomirov, Princeton University
Title: The spectral radius of a random matrix with heavy-tailed entries
Abstract: Consider a square matrix with independent and identically
distributed entries of zero mean and unit variance. It is well known
that if the entries have a finite fourth moment, then, in high
dimension, with high probability, the spectral radius is close to the
square root of the dimension. We conjecture that this holds true under
the sole assumption of zero mean and unit variance, in other words
that there are no outliers in the circular law. In this work we
establish the conjecture in the case of symmetrically distributed
entries with a finite moment of order larger than two. The proof uses
the method of moments combined with a novel truncation technique for
cycle weights that might be of independent interest. This is a joint
work with Charles Bordenave, Pietro Caputo and Djalil Chafaï.
Tuesday, April 4, 4:15 PM, Rm. 5417
Speaker: Martin Zerner, University of Tuebingen
Title: Recurrence and transience of contractive autoregressive
processes and related Markov chains
Abstract: We characterize recurrence and transience of nonnegative
multivariate autoregressive processes of order one with random
contractive coefficient matrix, of subcritical multitype Galton-Watson
branching processes in random environment with immigration, and of the
related max-autoregressive processes and general random exchange
processes. Our criterion is given in terms of the maximal Lyapunov
exponent of the coefficient matrix and the cumulative distribution
function of the innovation/immigration component.
Tuesday, May 2, 4:15 PM, Rm. 5417
Speaker: Matthew Junge, Duke University
Title: The bullet problem with discrete speeds
Abstract: A bullet is fired along the real line each second with independent uniformly random speeds from [0,1]. When two bullets collide they mutually annihilate. The still open bullet problem asks if the first bullet ever survives. We establish survival in the variant where speeds are discrete. Joint with Brittany Dygert, Christoph Kinzel, Annie Raymond, Erik Slivken, and Jennifer Zhu.
Tuesday, May 9, 4:15 PM, Rm. 5417
Speaker: Moumanti Podder, Courant Institute, NYU
Title: Rogue Fixed Points of Tree Automata on Galton-Watson Trees
Co-authors: Joel Spencer, Tobias Johnson and Fiona Skerman
Abstract: This talk will focus on tree automata, which are tools to analyze existential monadic second order properties of rooted trees. A tree automaton 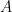 consists of a finite set
consists of a finite set 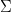 of colours, and a map
of colours, and a map  . Given a rooted tree
. Given a rooted tree  and a colouring
and a colouring  , we call
, we call  compatible with automaton
compatible with automaton 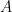 if for every
if for every 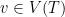 , we have
, we have  , where
, where 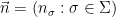 and
and 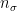 is the number of children of
is the number of children of  with colour
with colour 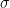 . Under the Galton-Watson branching process set-up, if
. Under the Galton-Watson branching process set-up, if  denotes the probability that a node is coloured
denotes the probability that a node is coloured 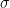 , then
, then  is obtained as a fixed point of a system of equations. But this system need not have a unique fixed point.
is obtained as a fixed point of a system of equations. But this system need not have a unique fixed point.
Our question attempts to answer whether a fixed point of such a system simply arises out of analytic reasons, or if it admits of a probabilistic interpretation. I shall formally define interpretation, and provide a nearly complete description of necessary and sufficient conditions for a fixed point to not admit an interpretation, in which case it is called rogue.

